Image Encryption for Privacy

Overview

Teaching: 30 min
Exercises: 30 min

Questions

• How do we encrypt bitmap images using Paillier encryption?

Objectives

• (Optional) Review of Paillier Homomorphic Encryption

• Describe the serial implementation of image encryption.

• Measure timing of the image encryption.

Image Encryption for Privacy

Problem Introduction

Objective: Encrypting an image to protect privacy before sending it to another party for computation/processing. The input is an image is a grayscale bitmap picture (PNG, JPG) and the output is an encrypted image in a JSON format.

Utilize files in /handson/phe_image/.

Optional Review of Paillier Homomorphic Encryption

Review of Paillier Homomorphic Encryption (PHE) from lesson 5. Homorphic Encryption’s goal is to protect the sensitive information bits during the transmission and processing phase without ever decrypting them for processing. It permits certain types of computations without decrypting the data.

PHE is an asymmetric encryption that utilizes two different keys, a private key for encrypting and a public key for decrypting. Do the following small hands-on demo of phe.paillier Python module

Explanation of paillier_tools:

• Key-related functions: keypair_dump_jwk, pubkey_load_jwk, privkey_dump_jwk
• Data saving/seloading: envec_dump_json, envec_load_json, enimg_dump_json, enimg_load_json

Small hands-on demo of phe.paillier Python module (generating keypair, encrypting, decrypting)

Run paillier_encrypt.ipynb to generate a private-public keypair to encrypt and decrypt. There should now be two files, phe_key.pub and phe_key.priv.

# pip install phe # use this if the library isn't already installed
import time
import json
import numpy as np
import matplotlib.image as mpimg
import paillier_tools
from phe import paillier
from phe.util import int_to_base64

# Generate the private and public key for Paillier Encryption.
pubkey, privkey = paillier.generate_paillier_keypair(n_length=2048)
pubkey_jwk, privkey_jwk = paillier_tools.keypair_dump_jwk(pubkey, privkey)
paillier_tools.write_file("phe_key.priv", privkey_jwk + "\n")
paillier_tools.write_file("phe_key.pub", pubkey_jwk + "\n")

Simple Encrypt Exercise

Make a program to encrypt a real number and save it to a disk file. Utilize phe_image/encrypt_number.py. This program should:

• read the public and private key files (func: read_file)
• load in a public key from a file (func: pubkey_load_jwk)
• make up a number and encrypt it (func: pubkey.encrypt)
• save encrypted number to a disk file (filename: mynumber.pcyrpt, func: envec_dump_json and write_file)

Solution

import os
# Part 1: Read saved public/private keypair
privkey_jwk = paillier_tools.read_file("phe_key.priv")
pubkey_jwk = paillier_tools.read_file("phe_key.pub")
pubkey, privkey = paillier_tools.keypair_load_jwk(pubkey_jwk, privkey_jwk)

# Part 2: Initialize a number and then encrypt it
m2 = 10.01578
M1 = pubkey.encrypt(m2)
print("Encryption completed.")

# Part 3: Save the encrypted number to a file
output_name = "mynumber.pcyrpt"
print("Output file:       ", output_name)

M1_json = paillier_tools.envec_dump_json(pubkey, [M1])
paillier_tools.write_file(output_name, M1_json)

Simple Decrypt Exercise

Make a program to decrypt the saved number and print it. Utilize phe_image/paillier_encrypt.ipynb. This program should:

• load a private key from a file (func: privkey_load_jwk)
• load the encrypted number from disk (filename: mynumber.pcyrpt, func: envec_load_json and read_file)
• decrypt it (func: privkey.decrypt)
• print the decrypted number

Solution

# load the encrypted messages
pubkey_Unused, M1_list = paillier_tools.envec_load_json(paillier_tools.read_file(output_name))

# decrypt
m1_list = [ privkey.decrypt(M) for M in M1_list ]

# save to disk:
print("Decrypted numbers:")
print(m1_list)

(End of review of Paillier Encryption.)

Characterizing Runtime of Paillier Encryption

Encrypt Timing for a Vector of Integers Exercise

Encrypt X number of scalars with pubkey.encrypt and observe timing. Edit /handson/phe_image/encrypt_vector.py and use encrypt_vector.slurm that runs it.

Solution

#!/usr/bin/env python3

"""
Timing for encrypting a vector of X integers using Paillier scheme

This scripts performs the following:
* Reads in the argument numScalars, which is the number of integers
* Generate a temporary private and public key (func:  paillier.generate_paillier_keypair(n_length=2048))
* Time how long it takes to encrypt numScalars integers in the vector
"""

import time
import json
import numpy as np
import matplotlib.image as mpimg
import paillier_tools
from phe import paillier
from phe.util import int_to_base64
import datetime
import argparse

# 1: Reads in the argument numScalars, which is the number of integers 
parser = argparse.ArgumentParser(description='Timing of Encryption of a Vector of X Integers')
parser.add_argument('--numScalars', type=int, help='The number of integers in the vector')  
args = parser.parse_args()
numScalars = args.numScalars
print("Timing for Encrypting a Vector of", numScalars, "integers")

# 2. generate keys
pubkey, privkey = paillier.generate_paillier_keypair(n_length=2048)

# 3. create a vector of X integers
x_plain = list(range(1, numScalars+1))
print("Plaintext x:", str(x_plain[:3]), "...", str(x_plain[-3:]))

# 4. Time encrypting vector
print("Encrypting", numScalars, "numbers...")
t0 = time.time()
X_enc = [ pubkey.encrypt(x1) for x1 in x_plain ]
t1 = time.time()
print("Time: Encrypting", numScalars, "integers = {}s".format(round(t1-t0, 3)))

Time: Encrypting 100 integers = 13.054s

Time: Encrypting 200 integers = 25.832s

Time: Encrypting 400 integers = 51.245s

Time: Encrypting 1000 integers = 129.042s

Decrypt Timing for a Vector of Integers Excerise

Decrypt X number of scalars with privkey.decrypt and observe timing. Create decrypt_vector.py and use decrypt_vector.slurm that runs it.

Solution

#!/usr/bin/env python3

"""
Timing for decrypting a vector of X integers using Paillier scheme

This scripts performs the following:
* Reads in the argument numScalars, which is the number of integers
* Generate a temporary private and public key (func:  paillier.generate_paillier_keypair(n_length=2048))
* Encrypt numScalars integers in the vector
* Time decrypting numScalars integers in the vector

"""

import time
import json
import numpy as np
import matplotlib.image as mpimg
import paillier_tools
from phe import paillier
from phe.util import int_to_base64
import datetime
import argparse

# 1: Reads in the argument numScalars, which is the number of integers 
parser = argparse.ArgumentParser(description='Timing of Encryption of a Vector of X Integers')
parser.add_argument('--numScalars', type=int, help='The number of integers in the vector')  
args = parser.parse_args()
numScalars = args.numScalars
print("Timing for Decrypting a Vector of", numScalars, "integers")

# 2. generate keys
pubkey, privkey = paillier.generate_paillier_keypair(n_length=2048)

# 3. create a vector of X integers
x_plain = list(range(1, numScalars+1))
print("Plaintext x:", str(x_plain[:3]), "...", str(x_plain[-3:]))

# 4. Encrypting vector
print("Encrypting", numScalars, "numbers...")
X_enc = [ pubkey.encrypt(x1) for x1 in x_plain ]

# 5. Time decrypting a vector of X integers
print("Decrypting", numScalars, "numbers...")
t0 = time.time()
X_dec = [ privkey.decrypt(x1) for x1 in X_enc ]
t1 = time.time()
print("Time: Decrypting", numScalars, "integers = {}s".format(round(t1-t0, 3)))

Time: Decrypting 100 integers = 3.769s

Time: Decrypting 200 integers = 7.455s

Time: Decrypting 400 integers = 15.186s

Time: Decrypting 1000 integers = 37.879s

Timing Discussion

Discuss the amount of wall time required for 1000, 1,000,000, etc numbers

Bitmap image encryption

The computer representation of a bitmap image is a 2-D array of values (0.255 in many cases of grayscale). Images are encrypted one pixel at a time.

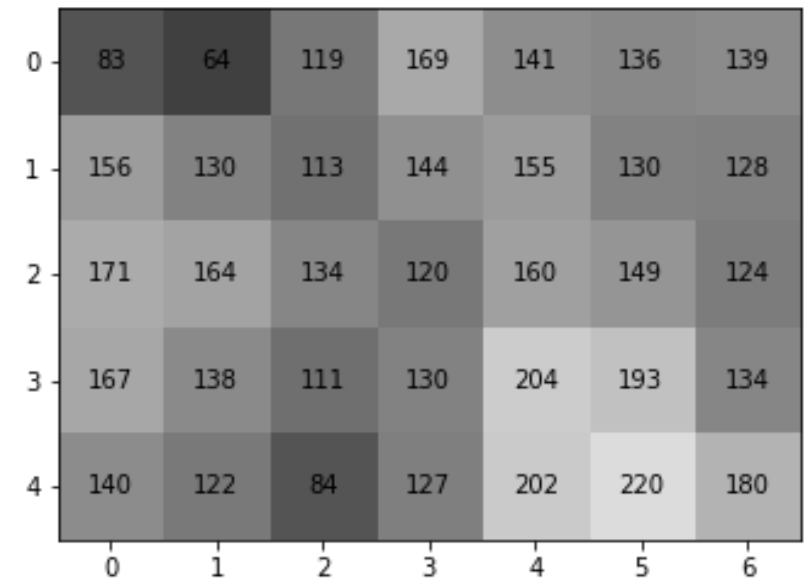
Figure: a bitmap image represented as a 2-D array representation.

Encrypt an Image Exercise

Encrypt an image pixel by pixel. See phe_image/encrypt_img.py. Load in lion14graytiny.jpg, which is a 39x26 grayscale image.

#!/usr/bin/env python3
"""
Image encryption using Paillier scheme

This scripts performs the following:
* loads an image
* converts to grayscale if needed
* encrypts the image
* writes encrypted image to a disk file (in JSON format).

"""
import datetime
import json
import re
import sys
import time

import numpy as np
import matplotlib.image as mpimg

from phe import paillier
from phe.util import int_to_base64
from paillier_tools import *

# Section: Initialize (loading in image, transform to grayscale,
# load key, preallocate array to contain encrypted pixels)

file_name = "lion14graytiny.jpg"

# Load the image
image_orig = mpimg.imread(file_name)

print("Image input file:        ", file_name)
print("Shape of original image: ", image_orig.shape)

# Transform to grayscale to reduce the computational workload
gray = convert_to_grayscale(image_orig)

n_rows = gray.shape[0]
n_cols = gray.shape[1]

print("Shape of data to be encrypted: ", gray.shape)

# Public key for encryption
pub_key = pubkey_load_jwk(read_file("phe_key.pub"))

# Preallocate array to contain encrypted pixels:
# Each element contains a single row of pixels.
gray_enc = [None] * n_rows

# Encryption Section: encrypt the pixels one by one
start = time.time()
n_enc = 0

print("Encrypting the pixels...")

for i in range(0, n_rows):
    print(" ", i, end="", flush=True)
    # Encrypt row values
    row_enc = [ pub_key.encrypt(float(x)) for x in gray[i] ]
    # Serialize row values for writing to JSON file
    gray_enc[i] = [(int_to_base64(x.ciphertext()), x.exponent) for x in row_enc]
    n_enc += len(gray_enc[i])

print(flush=True)

date = datetime.datetime.now().strftime('%Y-%m-%dT%H:%M:%S')

print("Encryption completed. ", n_enc, " pixels were processed.")

# Section: Save the encrypted 2-D array to a file
# Compute output filename
output_name = file_name.rsplit(".", 1)[0] + ".pcrypt"
print("Image output file:       ", output_name)
comment = 'Encrypted on ' + date

# Store a lot of metadata so we can comprehend the file later on
enimg_dump_json(pub_key, gray_enc, gray.shape, image_orig.shape, comment, output_name)

end = time.time()

# Print total execution time
print("Timing: Completed in ", end - start, "seconds.")

Decrypt an Image Exercise

Decrypt an image pixel by pixel. See phe_image/paillier_encrypt.ipynb. Decrypt the encoded lion14graytiny.jpg saved file and display it.

#!/usr/bin/env python3

"""
Image decryption using Paillier scheme

This scripts performs the following:
* loads in the private key
* use the private key to load in the encrypted json file
* change the encrpyted data into EncryptedNumbers, then decrypt row values
* display the image

"""

import datetime
import json
import re
import sys
import time

import numpy as np
import matplotlib.image as mpimg

from phe import paillier
from phe.util import int_to_base64
from paillier_tools import *

# Load in keys
privkey_jwk = paillier_tools.read_file("phe_key.priv")
pubkey_jwk = paillier_tools.read_file("phe_key.pub")
pub_key, priv_key = paillier_tools.keypair_load_jwk(pubkey_jwk, privkey_jwk)

# load in the encrypted json file
pubkey_d, enc_img, shape = enimg_load_json("lion14graytiny.pcrypt")

imgArray = [] # will hold the decrypted pixels
n_dec = 0

# Do work: decrypt the pixels one by one
start = time.time()
for i in range(0, n_rows):
    print(" ", i, end="", flush=True)
    # Change the encrpyted data into EncryptedNumbers, then decrypt row values
    values_d = [
        paillier.EncryptedNumber(pubkey_d, ciphertext=phe.util.base64_to_int(v[0]), exponent=int(v[1]))
        for v in enc_img[i]
    ]
    row_dec = [ int(priv_key.decrypt(x)) for x in values_d]
    imgArray.append(np.array(row_dec, dtype=np.uint8)) # needs to be in uint8 format
    n_dec += len(row_dec)
print("\nDecryption completed. ", n_dec, " pixels were processed.")
imgArray = np.array(imgArray, dtype=np.uint8) # needs to be in uint8 format

# display the image
from PIL import Image
im = Image.fromarray(imgArray)
im.show()
end = time.time()

# Print total execution time
print("Timing: Completed in ", end - start, "seconds.")

The Jupyter notebook should output/show the following image.

Figure: lion14graytiny.jpg

This was the original image, so you have now successfully encrypted and decrypted the image of the lion.

Timing Sections of Encrypting Image Exercise

Add timing information to phe_image/encrypt_img.py. The solution is included in the paillier_encrypt.ipynb.

1. Initialize (loading in image, transform to grayscale, load key, preallocate array to contain encrypted pixels

2. Encryption of image pixel by pixel

3. Save the encrypted image to a file

Solution

Initialization Section: 0.0026 seconds.

Work Section Encrypt (26, 39): 131.9641 seconds.

Save to File Section: 0.0229 seconds.

Full runtime: 131.9897 seconds.

Encryption Timing Discussion

Discuss the amount of time required to save an encrypted 400 x 256 or a full HD 1920 x 1080, etc. sized image.

Key Points

• You can use phe.paillier Python module to encrypt and decrypt images using Paillier Homomorphic Encryption.