Parallel Computation of Statistics of a Large Array

Overview

Teaching: 30 min
Exercises: 30 min

Questions

How do we convert a serial program to a parallel program using MPI?

Objectives

Demonstrate the step-by-step conversion of a serial program to a parallel program.

Create a parallel program that computes statistics on a large array from the given serial code.

Investigate parallel speedup and introduction to Amdahl’s Law.

Identify multiple ways to improve (in terms of runtime) the parallel code.

Improvement by utilizing compiled-language routines/libraries instead of pure Python

Parallel Computation of Statistics of a Large Array

Problem Introduction

Execute rand_reduction.py, that computes the mean and standard deviation of a large set of random numbers (N=10,000,000) in serial (and afterwards, in parallel). First, we will gain an understanding of the serial code (rand_reduction.py) and note the total time. Run the code three times to get an idea of the real run time (there is a fluctuation in the timing). Second, identify and then add timing for the different sections of code. Third, change the serial code into parallel.

Part 1: Exploring the serial version of the serial code

Navigate to /handson/reduction/. This code is saved under rand_reduction.py (and rand_reduction.slurm).

#!/usr/bin/env python3
# rand_reduction.py computes the mean and standard deviation
# of a large set of random numbers in serial.
#

import sys
import time
import numpy

startTime = time.time()

# Randomly generate numbers to sum over:
COUNT = 10000000
SEED = COUNT    #random seed is the same as COUNT

# We use a hard-coded random seed so the random numbers are always identical
# across all runs.
numpy.random.seed(SEED)
NUMBERS = numpy.random.random((COUNT,))

# numbers_w will be the array of data assigned to this worker
# to sum over:
numbers_w = NUMBERS

print("Sum", len(numbers_w), "numbers")
if len(numbers_w) > 6:
    print("Numbers to sum: ", numbers_w[:3], "...", numbers_w[-3:])
else:
    print("Numbers to sum: ", numbers_w)

# Compute the sum of the numbers (--> sum_w)
# and the sum of the square of the numbers (--> sum2_w).
# We could have used the `sum` built-in function here;
# but we choose the slower route so that we can "feel" the work.
sum_w = 0
sum2_w = 0
for n in numbers_w:
    sum_w += n
    sum2_w += n * n

# Report the temporary results here
print("Sum of numbers: ", sum_w)
print("Sum of squares: ", sum2_w)

ALL_SUM = sum_w
ALL_SUM2 = sum2_w

STD_DEV = numpy.sqrt(ALL_SUM2 / COUNT - (ALL_SUM/COUNT)**2)

endTime = time.time()

print("Total sum of all the numbers = ", ALL_SUM)
print("Average of all the numbers   = ", ALL_SUM/COUNT)
print("Std dev of all the numbers   = ", STD_DEV)
print("Total run time               = {:.3f} s".format(endTime - startTime))

(Total) Serial Timing Exercise

Run rand_reduction.py using rand_reduction.slurm four times and note the total time. This gives an idea of the real run time, since there is a slight fluctuation in the timing per run.

Solution

Run 1: 4.179s, Run 2: 4.004s, Run 3: 4.004s, and Run 4: 4.165s. Average total run time is 4.088 seconds.

# Example output for one file
Run rand_reduction in serial.
Sum 10000000 numbers
Numbers to sum:  [0.13810768 0.56165018 0.1325986 ] ... [0.79628671 0.83830487 0.23230454]
Sum of numbers:  4999942.139354685
Sum of squares:  3333616.437725455
Total sum of all the numbers =  4999942.139354685
Average of all the numbers   =  0.49999421393546856
Std dev of all the numbers   =  0.28873418537401907
Total run time               = 4.179 s

# Just the timing information from the next run.
...
Total run time               = 4.004 s

# Just the timing information from the next run.
...
Total run time               = 4.004 s
# Just the timing information from the next run.
...
Total run time               = 4.165 s

So, the average total run time for the above example output is 4.088 seconds. This average calculation can be computed using the ReductionNotebook.ipynb.

Part 2A: Identify sections of the serial code

Find the different sections of code following the simple parallel code template from the previous episode.

Sections of the Serial Code Exercise

Identify the sections of code and then calculate the time in each section.

Part 1: Initialization.

Part 2: Work.

Part 3: Results/Summary.

Solution

Part 1: Initialization

Random numnber generation: initialize the size, COUNT, SEED, and NUMBERS variables.

Part 2: Work

Computation of the sums and standard deviation. The sum of numbers (sum_w) and the sum of the square of the numbers (sum2_w).

Computation of the standard deviation (STD_DEV).

Part 3: Results/Summary

Final summary and report. The print statements for total sum, average, standard deviation and total run time.

Part 2B: Timing the Different Sections of Code

Create a new python file rand_reduction_timing.py from rand_reduction.py that allows the printing of the timing for each part.

Add the following lines of code to produce the timings for the first and second sections.

# numbers_w will be the array of data assigned to this worker to sum over:
numbers_w = NUMBERS

# Starting of the work section. Computing the two sums and standard deviation.

startWorkTime = time.time()
initTime = startWorkTime - startTime

endTime = time.time()
computeTime = endTime - startWorkTime

print("Total sum of all the numbers = ", ALL_SUM)
print("Average of all the numbers   = ", ALL_SUM/COUNT)
print("Std dev of all the numbers   = ", STD_DEV)
print("Input generation time        = {:.3f} s".format(initTime))
print("Compute time                 = {:.3f} s".format(computeTime))
print("Total run time               = {:.3f} s".format(endTime - startTime))

Use rand_reduction_timing.slurm to get the timing information for each section. The output section timings demonstrate that we should focus on trying to parallelize the work section.

# Run rand_reduction_timing in serial.
Sum 10000000 numbers
Numbers to sum:  [0.13810768 0.56165018 0.1325986 ] ... [0.79628671 0.83830487 0.23230454]
Sum of numbers:  4999942.139354685
Sum of squares:  3333616.437725455
Total sum of all the numbers =  4999942.139354685
Average of all the numbers   =  0.49999421393546856
Std dev of all the numbers   =  0.28873418537401907
Input generation time        = 0.106 s
Compute time                 = 3.904 s
Total run time               = 4.009 s

Part 3: Serial to Parallel Code

Which section takes the longest time? The sections of code that run slow are good candidates for parallelization. Let’s try to parallelize this section to reduce the time. Note the differencing in timing between the serial and parallel versions of the code.

Parallel Code Speedup Exercise 1

CHALLENGE: On your own, parallelize the serial code and save it as rand_reduction_par.py and utilize rand_reduction_par.slurm, which runs rand_reduction_par.py using 1, 2, 8, and 16 parallel resources.

Keep the following in mind when parallelizing the code.

MPI initialization (size and rank)
Broadcast the input data (COUNT, SEED, NUMBERS)
- Optional: Don’t broadcast the variables yet
Figure out the work domain for each worker. In other words, the workload for each worker. Hint: import range_decomp function created in the previous episode and adapt it here.
- Optional: do this in parallel for all workers, figure their own respective workloads. Hint: use scatter operation to distribute NUMBERS, or do it serially and scatter the work domains
Add gather/reduce operations to sum up all the partial sums (from each worker)

Solution

A simplistic version of the parallelized code, rand_reduction_par.py, is included. There are opportunities for improvement, it is just meant to be a simple example that demonstrates good parallel speedup.

#!/usr/bin/env python3
# Parallel version of rand_reduction.py Performs a sum of `COUNT` random numbers and calculates its standard deviation.
#
# Wirawan's parallel version #2 (2021-02-08)
# * Using range_decomp version "1"
# * Arrays are replicated across workers
# * Using mpi_send to ship out only array bounds
#
"""
Simplistic MPI parallelized version of rand_reduction.py that can be improved.

* No specific-part timings
* Data array was not distributed, but replicated
"""

import sys
import time
import numpy

from mpi4py import MPI

t1 = time.time()

# MPI initialization
comm = MPI.COMM_WORLD
size = comm.Get_size()
rank = comm.Get_rank()

# Randomly generate numbers to sum over: but with definite seed
# to let us compare results
if rank == 0:
    COUNT = 10000000
    SEED = COUNT    # random seed is the same as COUNT

    numpy.random.seed(SEED)
    NUMBERS = numpy.random.random((COUNT,))
else:
    # Assign them with dummy values because the var names must exist
    # on bcast below
    COUNT = None
    SEED = None
    NUMBERS = None

# Replicate the following data to all workers
count_g = comm.bcast(COUNT, root=0)
seed_g = comm.bcast(SEED, root=0)
numbers_g = comm.bcast(NUMBERS, root=0)

t2 = time.time()
gen_time = t2 - t1

### PROBLEM DECOMPOSITION
# Decompose the range into pieces for each worker to process

if rank == 0:
    # determine array's lower and (exclusive) upper bounds 
    L = [ 0 ] * size
    U = [ 0 ] * size
    for r in range(size):
        L[r] = COUNT * r // size
        U[r] = COUNT * (r + 1) // size

# Divvy up work: use sends (to all other worker nodes) and
# receive on the other worker's end

if rank == 0:        
    for r in range(1, size):
        comm.send(L[r], dest=r, tag=1)
        comm.send(U[r], dest=r, tag=2)

    # pass on the local worker's data:
    lb_w = L[0]
    ub_w = U[0]
else:
    lb_w = comm.recv(source=0, tag=1)
    ub_w = comm.recv(source=0, tag=2)

# Get the portion of the work on each worker
# numbers_w will be the array of data assigned to this worker
# to sum over:
numbers_w = numbers_g[lb_w : ub_w]

# beware that the indices in numbers_w will be 0, 1, 2, ... again
# and not lb_w, lb_w+1, ...

print("Rank", rank, "will sum", len(numbers_w), "numbers")
if len(numbers_w) > 6:
    print("Rank", rank, ": numbers to sum: ", numbers_w[:3], "...", numbers_w[-3:])
else:
    print("Rank", rank, ": numbers to sum: ", numbers_w)

### DO WORK HERE
# Do the sum in parallel

# Compute the sum of the numbers (--> sum_w)
# and the sum of the square of the numbres (--> sum2_w).
# We could have used the `sum` built-in function here;
# but we choose the slower route so that we can "feel" the work.
sum_w = 0
sum2_w = 0
for n in numbers_w:
    sum_w += n
    sum2_w += n * n

# Report the temporary results here
print("Rank", rank, ": sum of numbers: ", sum_w)
print("Rank", rank, ": sum of squares: ", sum2_w)

# get back all the local sums to the master process to finalize
# use the "reduce" operation

ALL_SUM = comm.reduce(sum_w, root=0)
ALL_SUM2 = comm.reduce(sum2_w, root=0)

t99 = time.time()
run_time = t99 - t1

if rank == 0:
    STD_DEV = numpy.sqrt(ALL_SUM2 / COUNT - (ALL_SUM/COUNT)**2)

    print("Total sum of all the numbers = ", ALL_SUM)
    print("Average of all the numbers   = ", ALL_SUM/COUNT)
    print("Std dev of all the numbers   = ", STD_DEV)
    print("Input generation time = {:.3f} s".format(gen_time))
    print("Total run time        = {:.3f} s".format(run_time))

Analyzing Parallel Code Speedup

There are always portions of the code that must be performed in serial. One way to calculate the amount of speedup due to parallelism, is to divide the total time taken in the serial version with the total time taken in the parallel version. Creating a graph can provide valuable information about how the number of workers affects the speedup.

Parallel Code Speedup

Compute scaling study by utilizing the output timing and ReductionNotebook.ipynb, which graphs the speedup vs. number of tasks.

Solution

Figure: Parallel speedup with 1, 2, 8, and 16 workers.

This concept is also known as parallel scaling: the execution time as a function of the number of processes. The ideal is linear scaling, but in practice, it is impossible to achieve because there are certain tasks that must be done in serial. An example is random number generation performed on rank 0.

This concepts leads to Amdahl’s Law. f is the fraction of the algorithm that can be parallelized, and S is the speedup.

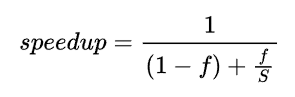
Speedup

Timing relating to communication is another reason that ideal speedup is not achievable in practice. To maximize speedup due to parallelization, reduce communication overhead and overlap communication with computations. In other words, you can use asynchronous MPI sends, receives, and other collectives. Another reason preventing ideal speedup is uneven workloads amongst workers. Uneven workloads will cause workers to have to wait on another to continue. Utilize problem decomposition to reduce uneven workloads.

Improving the Parallel Efficency

Improving the Parallel Code Exercise

Identify the time-consuming serial computation in the parallel code.

Identify time-consuming communication in the parallel code.

Solution

The most time-consuming serial computation is the random number computation on master rank

The random number (big array) broadcasting from the master rank is the most time-consuming communication.

With that in mind, let’s think of how best to improve the parallel code. First, use scatter instead of broadcast to distribute the big data instead of replicating them. This also saves worker’s memory. Second, independently generate random numbers for each worker. However, this gives up 100% numerical reproducibility.

Now, let’s implement these changes. For numbers_g, scatter the data amongst the workers. Distributing the data in this manner means that the original numbers are generated on rank 0, and each worker receives only the relevant portion of data to work on. This is known as data parallelism.

Scope of Data: Replicated vs Distributed vs Rank 0

Type of Data	Information	Variables
Global, replicated	Same value on all processes	count_g, numbers_g
Private, distributed	Different values on different processes and only relevant portion of the entire data	lb_w, ub_w, numbers_w, loop variables, and other variables
Global Rank 0 Only	Only defined and valid on rank 0 process	COUNT, NUMBERS

Still generate NUMBERS on Rank 0
Use scatter operation to feed workers with only their respective parts of the data

Improving Performance

Use compiled-language routines/libraries instead of pure Python.

Use numpy function to replace the hand-written loop to compute the sum (sum_w, sum2_w)
- Whenever possible, use numpy functions to process lots of numbers / data
  - Functions in libraries like numpy are implemented in C, C++, and/or Fortran
  - C/C++ codes can run ~ 50x faster
  - Do this first before parallelization

These can be implemented by replacing the following.

+ sum_w = numpy.sum(numbers_w)
+ sum2_w = numpy.sum(numbers_w**2)
- sum_w = 0
- sum2_w = 0
- for n in numbers_w:
-     sum_w += n
-     sum2_w += n * n 

Implement Improving Performance (to Serial Code)

Replace the hand-written loop to compute the sum with numpy functions as described above. Utilize rand_reduction_improved.py and rand_reduction_improved.slurm. Compare the runtime for the improved serial version and the parallel program version.

Solution

0.147s runtime for the improved serial version of code, so the priority should be utilizing compiled-language routines/libraries instead of pure Python.

The priority is to use compiled-language routines/libraries instead of pure Python, since they will reduce runtime. Implementing the change to the serial code improved runtime more than utilizing 16 workers.

Key Points

Parallel code speedup analysis and why ideal cannot be achieved.

Be able to identify sections of code to improve to reduce runtime.

The priority is to use compiled-language routines/libraries instead of pure Python, since they will reduce runtime.

previous episode

DeapSECURE module 6: Parallel and High-Performance Programming

next episode

Parallel Computation of Statistics of a Large Array

Overview