Post-Analysis for Modeling Tuning Experiments
Overview
Teaching: 15 min
Exercises: 50 minQuestions
How should we visualize the outputs from the post-processing phase?
What general trends do we observe from the last epoch results?
Objectives
Understand the effect of tuning the different hyperparameters.
Acquiring the art and common sense of the hyperparameter tuning.
Introduction
Post-analysis is a very important part of machine learning tuning experiments. It follows the post-processing phase and focuses on analyzing the model’s results to better understand the behavior of a model and improve its performance.
The experimental results we will perform post-analysis on come from Tuning Neural Network Models for Better Accuracy (herein referred to as the “model tuning episode”), where we conducted machine learning experiments using Jupyter Notebook, and from Effective Deep Learning Workflow on HPC (herein referred to as the “HPC model tuning episode”), where we utilized batch training on the HPC. These experiments utilize the following baseline model.
The Baseline Model
As a reminder, the baseline model for tuning the
sherlock_18appsclassifier is defined with the following hyperparameters:
- One hidden layer with 18 neurons;
- Learning rate of 0.0003;
- Batch size of 32;
- 10 epochs (and 30 epochs for the batch HPC training lesson).
Our four types of experiments varied only one hyperparameter at a time. The first type varied the number of hidden neurons in the hidden layer. The second type varied the learning rate. The third type varied the batch size. The fourth type varied the number of hidden layers (while keeping the number of hidden neurons per layer constant).
The goal of these experiments is to observe the effects of increasing and decreasing one hyperparameter on the model’s accuracy. From these observations, we will draw conclusions and try to better optimize the model’s accuracy.
Takeaways from Tuning Experiments Part 1: Varying Hidden Layers
In the first type of experiment, we tuned the NN_Model_1H model
by varying only the number of neurons in the hidden layer,
the hidden_neurons hyperparameter.
Recall that the number of neurons in a hidden layer represents the
width of the layer.
More neurons increases the complexity of the model and vice versa.
Visualizing the results
Utilize post_analysis_NN_Model_1H.ipynb, which is recreated below.
This notebook assumes post-processing (steps 1-3) are already completed
for both model tuning episodes.
As a reminder, the result of the 3rd step of post-processing
was a saved CSV file that contained the metadata and output information.
It also creates different visualizations for the two model tuning episodes,
since the number of epochs is different.
Note:
Though the
post_analysis_NN_Model_1H.ipynbincludes code to visualize the model output from both episodes, only the results from the batch HPC episode will be shown. Both episodes require separate comparisons since the number of epochs was different.
Step 0: Import Modules and Define Helper Functions
import os
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
## Returns the last epoch data frame
#modelType - what it is called in the Model_Type column
#colName - the name of the column in the data frame
#dirName - name from the directory
#xLabel - Label for the graph
#last_epoch_data - the dataframe that only contains the last epoch data
def getResults(modelType, colName, dirName, xLabel, last_epoch_data):
# filter by the model type (the hyperparameter scanned)
last_epoch_data4 = last_epoch_data[last_epoch_data['Model_Type'].str.contains(modelType)]
# only include the loss, accuracy, val_loss, and val_accuracy columns
last_epoch_data3 = last_epoch_data4.iloc[:, 6:]
# If the type is "neurons," change it so that it is a single number. This will help when sorting by value.
if modelType == "neuron":
last_epoch_data4['neurons'] = last_epoch_data4['neurons'].str.replace('[^0-9]', '', regex=True).astype('int32')
# make the singular index the given scanned hyperparameter column, sort it, and print
last_epoch_data3.index = last_epoch_data4[colName]
last_epoch_data3 = last_epoch_data3.sort_index(axis=0)
if modelType != "layers": # do not print here because the string needs to be sorted which is done later
print(last_epoch_data3)
return last_epoch_data3
## Create the line plot
# last_epoch_data3 - data frame with data to graph
#dirName - name from the directory
#xLabel - Label for the graph
#toSave - whether to save the graphic
#includeLoss - whether to include loss in the graph
#logScale - whether the x-axis should be log scaled
#addString - optional additional string to add to the saved file name
def getLinePlot(last_epoch_data3, dirName, xLabel, toSave=True, includeLoss = True, logScale=False, addString = ""):
# if including the loss in the graph
if includeLoss:
fig, axes = plt.subplots(nrows=2,ncols=2)
# Loss and validation loss in the first column
last_epoch_data3.iloc[:, 0::2].plot(ylabel="Metric", xlabel=xLabel, marker='o', ax = axes[:,0], subplots=True)
ax1 = axes[:, 1]
else:
# creates only a subplot with the accuracy
fig, axes = plt.subplots(nrows=1, ncols=2)
ax1 = axes
# format the graph
plt.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=0.4, hspace=0.4) # create space between the plots
# accuracy and val_accuracy in the 2nd column
if includeLoss:
newTitle = 'Comparison of Model Performance for the Last Epoch: '
else:
newTitle = 'Comparison of Model Accuracy for the Last Epoch: '
last_epoch_data3.iloc[:, 1::2].plot(title=newTitle+xLabel, ylabel="Metric", xlabel=xLabel, marker='o', ax = ax1, subplots=True)
# if x-axis should be log scaled
if logScale:
for ax in axes:
ax.set_xscale('log')
# save the graph
if toSave:
if includeLoss:
endTitle = "last_epoch_loss_acc_plot.png"
else:
endTitle = "last_epoch_acc_plot.png"
if "Hidden Neurons" in xLabel:
plt.savefig("scan-"+dirName+"-02/"+addString+endTitle)
else:
plt.savefig("scan-"+dirName+"/"+addString+endTitle)
return fig,axes
## Create the bar graph
# last_epoch_data3 - data frame with data to graph
#dirName - name from the directory
#xLabel - Label for the graph
#toSave - whether to save the graphic
#includeLoss - whether to include loss in the graph
#logScale - whether the x-axis should be log scaled
#addString - optional additional string to add to the saved file name
def getBarGraph(last_epoch_data3, dirName, xLabel, toSave=True, includeLoss = True, logScale=False, addString=""):
# Create a bar chart (another way of displaying the results)
# Set the width and height of the bar chart
bar_width = 0.15
bar_positions = range(len(last_epoch_data3))
# if including loss in the plot
if includeLoss:
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15, 10))
# get the data from the data frame last_epochs_data3 and from the appropriate columns
ax[0].bar([pos - 2*bar_width for pos in bar_positions], last_epoch_data3['loss'], width=bar_width, label='Loss')
ax[0].bar([pos - bar_width for pos in bar_positions], last_epoch_data3['val_loss'], width=bar_width, label='Val Loss')
# Set x-axis ticks and labels
ax[0].set_xticks(bar_positions)
ax[0].set_xticklabels(last_epoch_data3.index)
# Add legend
ax[0].legend()
# Set title and labels
ax[0].set_title('Comparison of Model Loss for the Last Epoch: ' + xLabel)
ax[0].set_xlabel(xLabel)
ax[0].set_ylabel('Metrics')
ax1 = ax[1]
else:
fig, ax = plt.subplots(figsize=(15, 10))
ax1 = ax
# Plot the bars for accuracy and val_accuracy
ax1.bar(bar_positions, last_epoch_data3['accuracy'], width=bar_width, label='Accuracy')
ax1.bar([pos + bar_width for pos in bar_positions], last_epoch_data3['val_accuracy'], width=bar_width, label='Val Accuracy')
# Set x-axis ticks and labels
ax1.set_xticks(bar_positions)
ax1.set_xticklabels(last_epoch_data3.index)
# Add legend
ax1.legend()
# Set title and labels
ax1.set_title('Comparison of Model Accuracy for the Last Epoch: ' + xLabel)
ax1.set_xlabel(xLabel)
ax1.set_ylabel('Metrics')
# Display the chart
plt.tight_layout()
if toSave:
if includeLoss:
endTitle = "last_epoch_loss_acc_plot_bar_graph.png"
else:
endTitle = "last_epoch_acc_plot_bar_graph.png"
if "Hidden Neurons" in xLabel:
plt.savefig("scan-"+dirName+"-02/"+addString+endTitle)
else:
plt.savefig("scan-"+dirName+"/"+addString+endTitle)
plt.show()
return fig, ax
# Creates both plots
# last_epoch_data3 - data frame with data to graph
#dirName - name from the directory
#xLabel - Label for the graph
#toSave - whether to save the graphic
#includeLoss - whether to include loss in the graph
#logScale - whether the x-axis should be log scaled
#addString - optional additional string to add to the saved file name
def getPlots(last_epoch_data3, dirName, xLabel, toSave=True, includeLoss = True, logScale=False, addString = ""):
fig,axes = getLinePlot(last_epoch_data3, dirName, xLabel, toSave, includeLoss, logScale, addString)
fig,axes = getBarGraph(last_epoch_data3, dirName, xLabel, toSave, includeLoss, logScale, addString)
# Read in the CSV file
def read_post_processing(csvPath):
df = pd.read_csv(csvPath, index_col=0) # read in the csv file and ignore the additional numbered column
# Create last epoch DataFrame.
# Filter the DataFrame to only get the rows where the index is the last epoch.
last_epoch_data = df.groupby('job_ID').tail(1) #assumes each model has a different unique job_ID
print(last_epoch_data)
return last_epoch_data
Step 4: Analysis Phase: Visualizing the Results
Let’s look at the last epoch data for each model. Since the models only vary one hyperparameter at a time, let’s create a graphical representation of the last epoch metrics (accuracy) vs. varying hyperparameter.
Step 4.1 Read in the CSV File that Contains the Model History and Model Metadata
path = 'post_processing_all_hpc_batch.csv'
df = pd.read_csv(path, index_col=0) # read in the csv file and ignore the additional numbered column
print(df)
# Create last epoch DataFrame.
# Filter the DataFrame to only get the rows where the index is the last epoch.
last_epoch_data = df.groupby('job_ID').tail(1) #assumes each model has a different unique job_ID
print(last_epoch_data)
### Get results for the experiment for varying the number of hidden nuerons in the 1st layer
last_epoch_data_nn = getResults("neuron", "neurons", "hidden-neurons", "Hidden Neurons", last_epoch_data)
# Step 4.2: Create visualizations of the experiments. This will be the last epoch metric (accuracy) vs. the varying hyperparameter
getPlots(last_epoch_data_nn, "hidden-neurons", "Hidden Neurons", True, True, False)
## You can also do things, such as sorting (by one of the result columns, such as loss)
print(last_epoch_data_nn.sort_values(['val_accuracy'], ascending=False))
Run the post-analysis for the hidden neurons experiment.
loss accuracy val_loss val_accuracy
neurons
512 0.002919 0.999606 0.009277 0.999249
1024 0.003308 0.999593 0.006825 0.999231
256 0.003840 0.999515 0.007077 0.999194
80 0.007796 0.998654 0.011362 0.998425
40 0.016035 0.996434 0.017410 0.996375
18 0.045203 0.990570 0.043723 0.990589
12 0.070112 0.985663 0.068991 0.985389
8 0.183243 0.952651 0.183629 0.950912
4 0.463814 0.907489 0.460035 0.910356
2 1.051278 0.682108 1.061323 0.682804
1 1.945121 0.319691 1.947505 0.320510
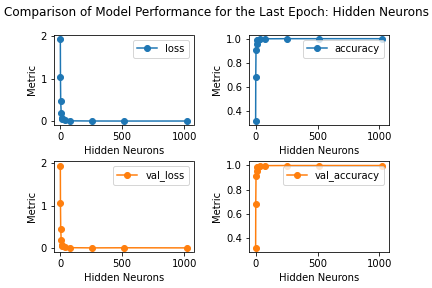
Figure: The model’s loss and accuracy for both the training and validation datasets as a function of the number of hidden neurons.
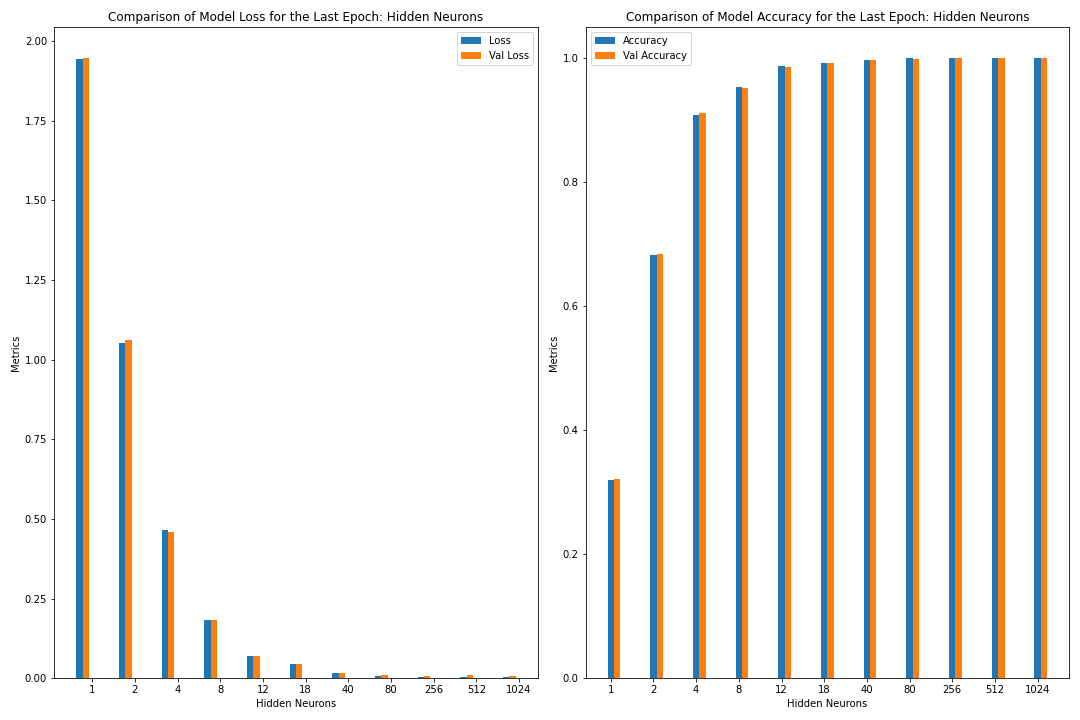
Figure: The model’s loss and accuracy for both the training and validation datasets as a function of the number of hidden neurons (as a bar graph).
What Did We Learn from the Tuning Experiments Part 1?
Let us recap what we learned from this experiments by answering the following questions:
What happened to the model’s accuracy when we reduce the
hidden_neuronshyperparameter? Describe the change in the accuracy of the model as we reduce thehidden_neuronshyperparameter to an extremely small number.What happened to the accuracy if we increase the
hidden_neuronshyperparameter? Discuss (or observe) what would happen if the hidden layer contains 1,000 or even 10,000 hidden neurons?In conclusion: In order to improve the accuracy of the model, should we use more or less hidden neurons?
Solutions
When the number of hidden neurons in a model is reduced, a discernible trend begins to emerge in the accuracy of the model. Initially, a modest reduction in the hidden layer resulted in moderately worse accuracy. Reducing the number of hidden neurons to extremely low numbers leads to a significant damage in the model’s accuracy. This marked drop-off signifies that the model’s capacity to learn complex patterns and nuances within the data has been significantly curtailed. With too few neurons, the model becomes overly simplistic, unable to adequately represent the diversity and intricacies present in the dataset, leading to a substantial deterioration in predictive performance.
Increasing the number of hidden neurons (from the baseline 18) increases the accuracy. Increasing the number of neurons increases the complexity of the model and computation time required.
In conclusion: While adding hidden neurons initially seems promising to improve accuracy, there is a point of diminishing returns beyond which the cost of improvements to accuracy outweighs the slight benefits to the model’s performance. In addition, increasing the number of hidden neurons may decrease due to overfitting or practical limitations. Finding the right balance in the number of hidden neurons is critical to achieving optimal model performance.
DISCUSSION:
What is an optimal value of
hidden_neuronsthat will yield the desirable level of accuracy? For example, what is the value ofhidden_neuronsthat will yield a 99% model accuracy? How about 99.5% accuracy? Can we reach 99.9% accuracy? Keep in mind that neural network model training is very expensive; increasing this hyperparameter may not improve the model significantly!
Modify the Post-Analysis to Only Show >= 18 neurons.
Modify the post-analysis to only show >= 18 neurons. Also, remove the loss information and only show the accuracy and val_accuracy metrics. This is because the loss visualization was already validated in the post-processing phase (i.e. the loss graphs did not show any abnormal behavior). The post-analysis phase focuses on performance metrics, in this case, accuracy and validation accuracy.
loss accuracy val_loss val_accuracy
neurons
18 0.045203 0.990570 0.043723 0.990589
40 0.016035 0.996434 0.017410 0.996375
80 0.007796 0.998654 0.011362 0.998425
256 0.003840 0.999515 0.007077 0.999194
512 0.002919 0.999606 0.009277 0.999249
1024 0.003308 0.999593 0.006825 0.999231
# Now, let's look at the results for the experiments where the number of neurons is greater than or equal to 18
# This should show how increasing the number of hidden neurons increases the accuracy
last_epoch_data3_temp = last_epoch_data_nn[last_epoch_data_nn.index >= 18]
print(last_epoch_data3_temp)
getPlots(last_epoch_data3_temp, "hidden-neurons", "Hidden Neurons >=18", True, False, False, "gr_18_")
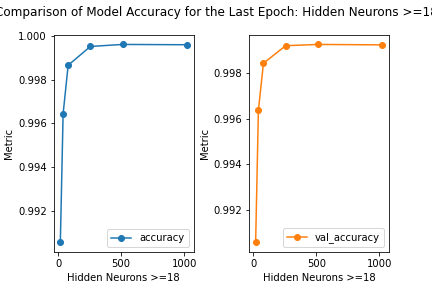
Figure: The model’s accuracy for both the training and validation datasets as a function of the number of hidden neurons where the number of neurons is greater than or equal to 18.
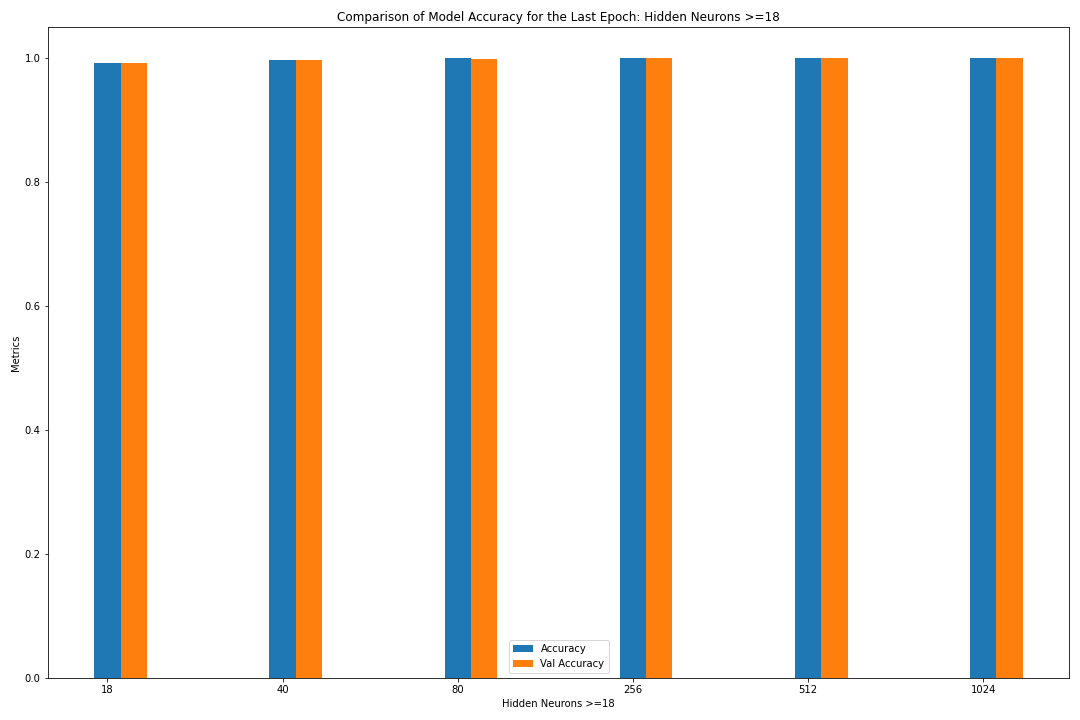
Figure: The model’s accuracy for both the training and validation datasets as a function of the number of hidden neurons where the number of neurons is greater than or equal to 18 (as a bar graph).
Deciding an Optimal Hyperparameter, Experiment 1: Varying Hidden Neurons
The example above shows a common theme with model tuning.
The more neurons we train, the more accuracy we can achieve
(subject to risk of overfitting, see below).
You should have observed that at large enough hidden_neurons,
the model accuracy started to level off
(i.e. adding more neurons will not give significant gain in accuracy).
Since training a neural network model is very expensive, we often have to make a trade-off between doing more trainings (which can be very costly, so may not be possible), and conserving effort against “point of diminishing return”, i.e. the point where improving the model does not yield a significant benefit in the model’s accuracy.
Where is the point of diminishing return?
This depends on the application. In some application we may really want to get as close as possible to 100%, then we have no choice but to train more (bite the bullet).
Takeaways from Tuning Experiments Part 2: Varying Learning Rate
In the second experiment above, we tuned the NN_Model_1H model
by varying the learning_rate hyperparameter.
Recall that the learning rate hyperparameter determines the step size.
In other words, it determines the amount that the model is able to
change after each iteration.
Run the post-analysis for the learning rate experiment.
### Create the graphs that compare the learning rate with the last epoch's metric.
modelType = 'lr' # what it is called in the Model_Type column
colName = 'learning_rate' # the name of the column in the data frame
dirName = 'learning-rate' # name from the directory
xLabel = "Learning Rate" # Label for the graph
last_epoch_data_lr = getResults(modelType, colName, dirName, xLabel, last_epoch_data)
getPlots(last_epoch_data_lr, dirName, xLabel, True, False, True)
## You can also do things, such as sorting (by one of the result columns, such as loss)
> print(last_epoch_data_lr.sort_values(['val_accuracy'], ascending=False))
loss accuracy val_loss val_accuracy
learning_rate
0.0010 0.018579 0.995926 0.021447 0.995862
0.0100 0.021298 0.995395 0.024532 0.995386
0.0003 0.045203 0.990570 0.043723 0.990589
0.1000 0.444514 0.921821 0.340468 0.921012
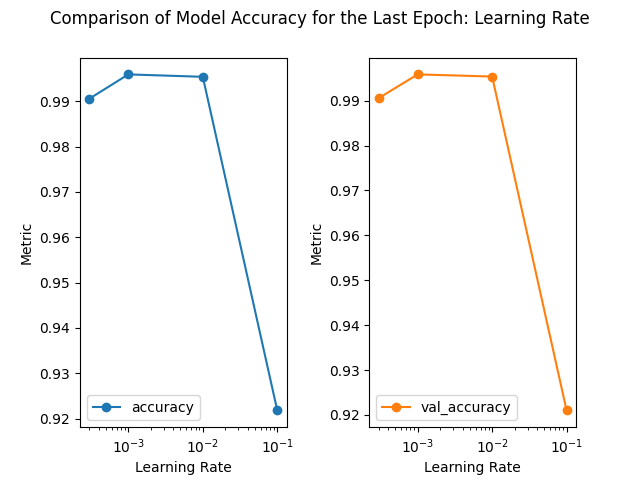
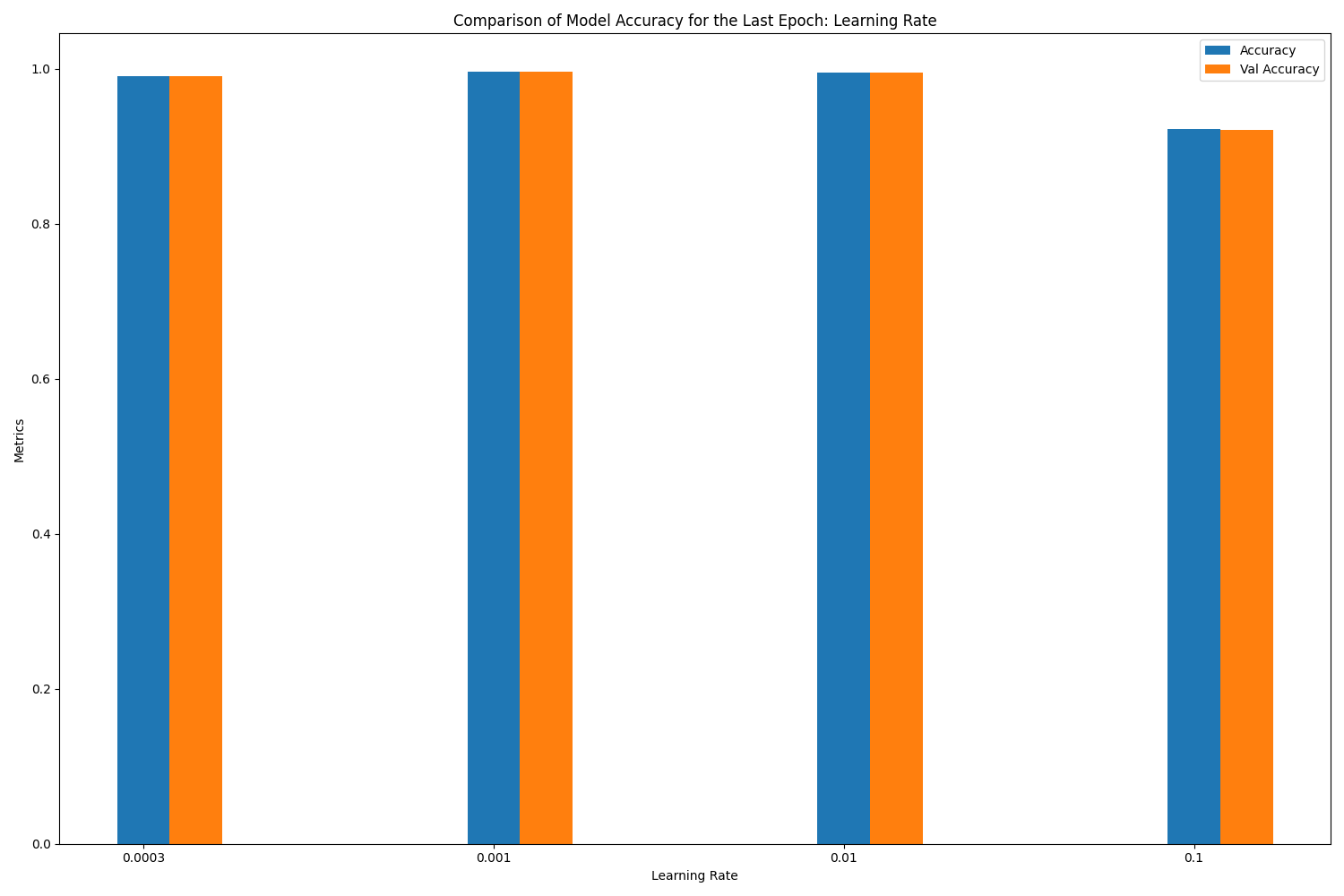
What did we learn from the Tuning Experiments Part 2?
Answer the questions below to recap what we learn about the effects of the learning rate.
1) What do you observe when we train the network with a small learning rate?
2) What happens to the training process when we increase the learning rate?
3) What happens to the training process when we increase the learning rate even further (to very large values)? Try a value of 0.1 or larger if you have not already.
4) What value of learning rate would you choose, and why?
ANSWERS:
1) When the learning rate is small, the updates to the weights and biases are small. This may cause the training process to converge slowly, requiring more iterations to achieve good results.
2) When the learning rate is large, the update magnitude of weights and biases increases, which can lead to faster training, up to a certain value of learning rate.
3) Beyond this sweet spot, oscillations or instability may occur during training, or even failure to converge to a good solution. Learning rate of 0.01 seems to be good, but the validation accuracy shows an oscillation toward the latter epochs. Learning rates of 0.1 or larger are indeed not good.
4) Important Takeaway: Choosing an appropriate learning rate is one of the key factors when training a neural network, and it needs to be adjusted and optimized according to specific problems and experimental results.
Takeaways from Tuning Experiments Part 3: Varying Batch Size
In the third experiment, we tuned the NN_Model_1H model
by varying the batch_size hyperparameter.
Recall that batch size is the number of training samples
used (in one iteration) to update the model’s parameters.
Run the post-analysis for the batch size experiment.
### Create the graphs that compare the batch size with the last epoch's metric.
modelType = 'batch' # what it is called in the Model_Type column
colName = 'batch_size' # the name of the column in the data frame
dirName = 'batch-size' # name from the directory
xLabel = "Batch Size" # Label for the graph
last_epoch_data_batch = getResults(modelType, colName, dirName, xLabel, last_epoch_data)
getPlots(last_epoch_data_batch, dirName, xLabel, True, False, True)
## You can also do things, such as sorting (by one of the result columns, such as loss)
print(last_epoch_data_batch.sort_values(['val_accuracy'], ascending=False))
loss accuracy val_loss val_accuracy
batch_size
16 0.023600 0.994557 0.023432 0.994763
32 0.045203 0.990570 0.043723 0.990589
128 0.071049 0.985741 0.070776 0.985224
64 0.062618 0.985123 0.064284 0.984968
512 0.164543 0.959549 0.161178 0.959133
1024 0.276155 0.930404 0.273338 0.931119
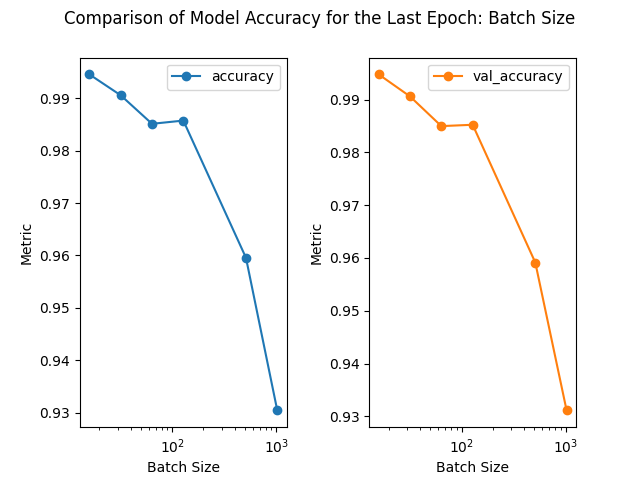
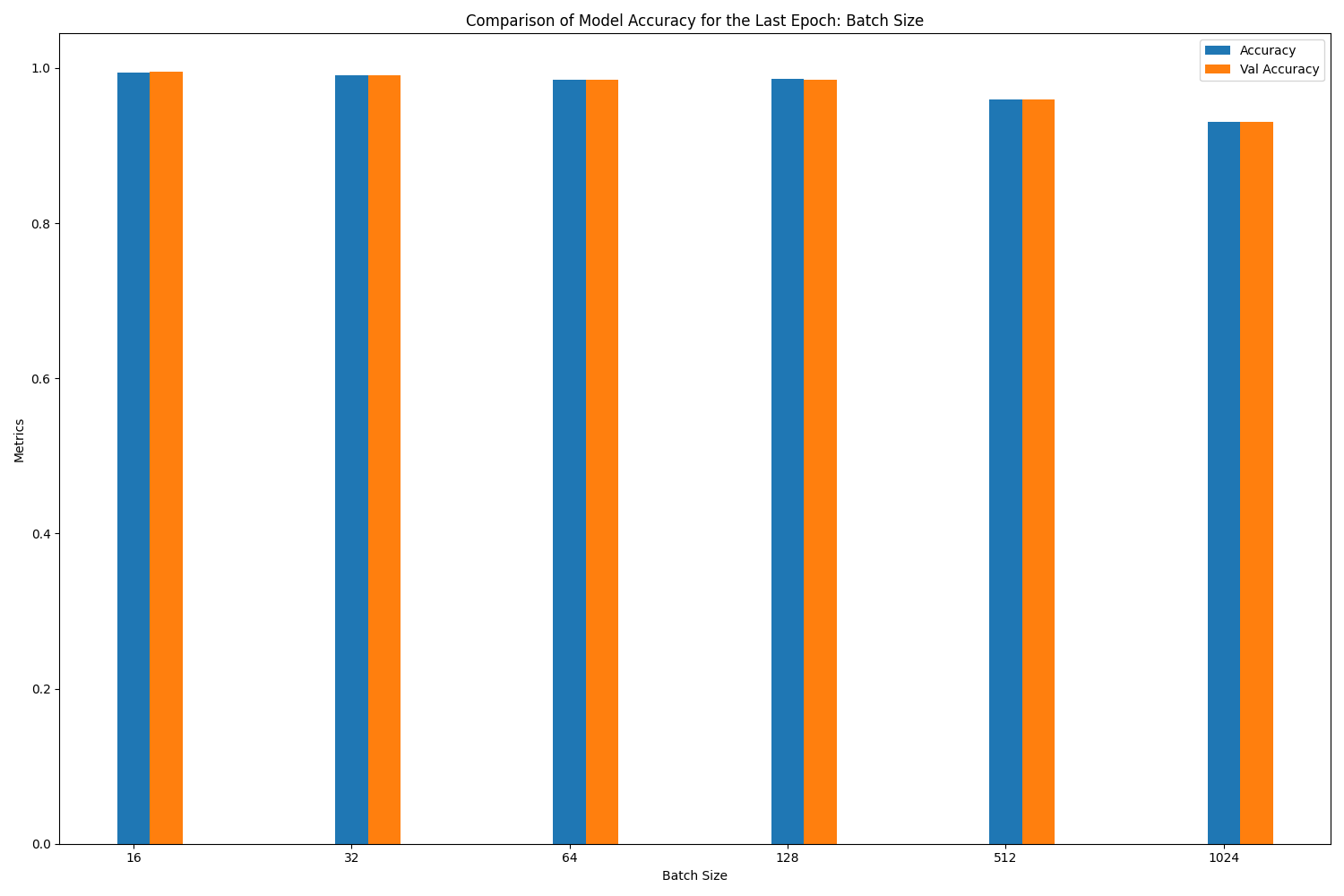
What did we learn from the Tuning Experiments Part 3?
Answer the questions below to recap what we learn about the effects of the learning rate.
1) What do you observe when the batch size changes?
2) How do you choose the right batch size?
ANSWERS:
1) As the batch size increases, although the training time is shortened, the accuracy rate decreases. This decrease in accuracy is more obvious with the results from the 1st lesson, where a batch size change from 16 to 1024 causes the validation accuracy to drop from 0.981 to 0.7573.
2) Common batch size choices are powers of 2 (e.g., 32, 64, 128, 256) due to hardware optimizations. However, there is no one-size-fits-all answer. It depends on the specific problem, dataset, model architecture, and available resources.
Takeaways from Tuning Experiments Part 4: Varying the Number of Hidden Layers
In the fourth experiment, we tuned the NN_Model_1H model
by varying the number of hidden layers hyperparameter (the number of hidden neurons in each layer still remain 18).
Recall that the number of hidden layers is usually referred to as the depth of the model.
More hidden layers increases the computational time.
It also increases the capability of the model to learn more complex patterns.
Run the post-analysis for the multiple layer experiment.
### Get results for the experiment for varying the number of layers
last_epoch_data_multipleNN = getResults("layers", "neurons", "layers", "Hidden Neurons with Multiple Layers", last_epoch_data)
# sort by the index: do this by changing the tuple to a list and then sorting by index
last_epoch_data_multipleNN.index = [x.replace('(', '[').replace(',)', ']').replace(')', ']') for x in last_epoch_data_multipleNN.index]
last_epoch_data_multipleNN = last_epoch_data_multipleNN.sort_index(ascending=False)
print(last_epoch_data_multipleNN)
# replot the graphic because we want to adjust the rotation of the x-axis labels
fig,axes = getLinePlot(last_epoch_data_multipleNN, "layers", "Multiple Layers", True, False, False)
for ax in axes:
ax.set_xticklabels(ax.get_xticklabels(), rotation=60)
# save the adjusted plot
endTitle = "last_epoch_acc_plot.png"
plt.savefig("scan-layers"+"/"+endTitle, bbox_inches='tight')
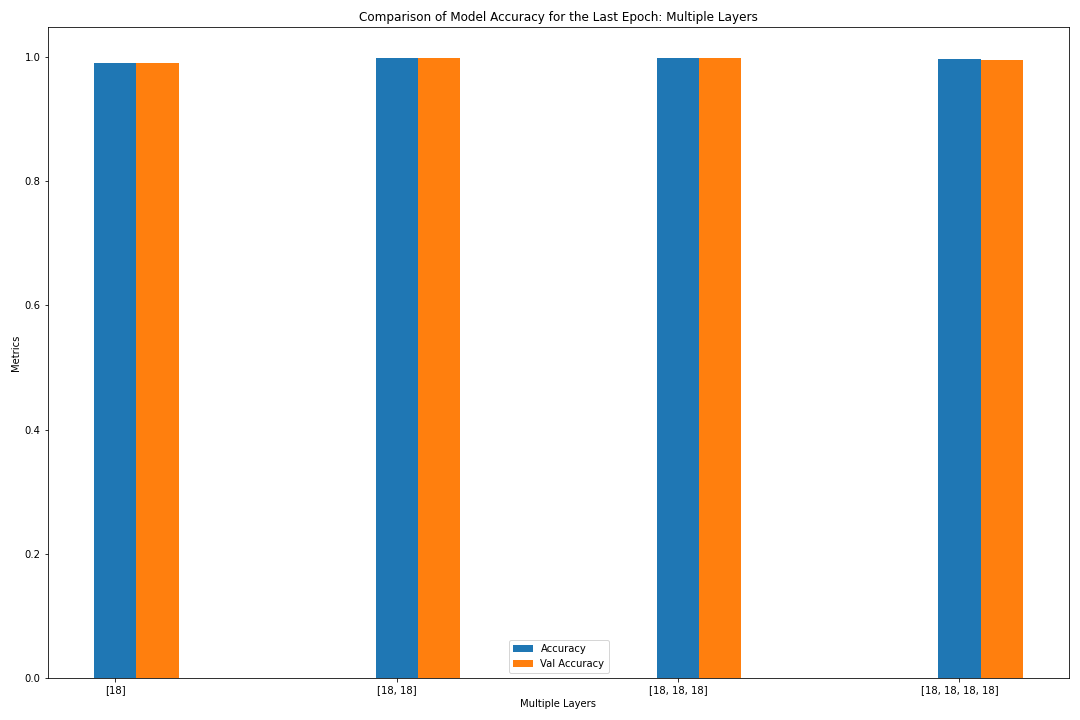
fig,axes = getBarGraph(last_epoch_data_multipleNN, "layers", "Multiple Layers", True, False, False)
print(last_epoch_data_multipleNN.sort_values(['val_accuracy'], ascending=False))
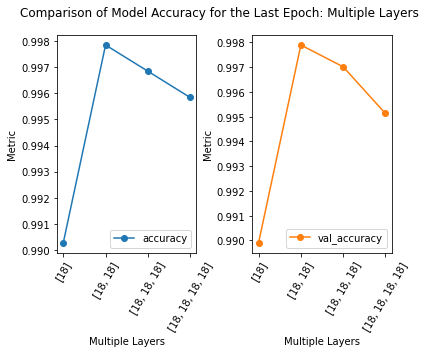
loss accuracy val_loss val_accuracy
neurons
[18, 18] 0.011239 0.997849 0.012328 0.997894
[18, 18, 18] 0.016116 0.996846 0.019097 0.997016
[18, 18, 18, 18] 0.018118 0.995839 0.020112 0.995130
[18] 0.043249 0.990277 0.043251 0.989911
What did we learn from the Tuning Experiments Part 4?
Answer the questions below to recap what we learn about the effects of the number of hidden layers.
1) How many neurons should be in each hidden layer?
2) What did you observe?
3) What do we learn from here?
ANSWERS:
1) The number of neurons to use in each hidden layer is problem dependent. It will take more experiments to determine the optimal number of neurons in each hidden layer.
2) The model with the least number of layers, and thus the least complex, performs the worst, according to the validation accuracy. The model with four layers performed the second to the worst, according to the validation accuracy. This is the type of experiment where we need to consider the point of diminishing return. Does the increased accuracy of the model between one and three hidden layers outweigh the additional computational cost?
3) Usually, the more neurons we train, the more accuracy we can get (subject to risk of overfitting, vanishing and exploding gradients).
While increasing the number of hidden layers in a neural network can potentially improve its ability to learn complex patterns and representations, it does not guarantee higher accuracy.
Summary
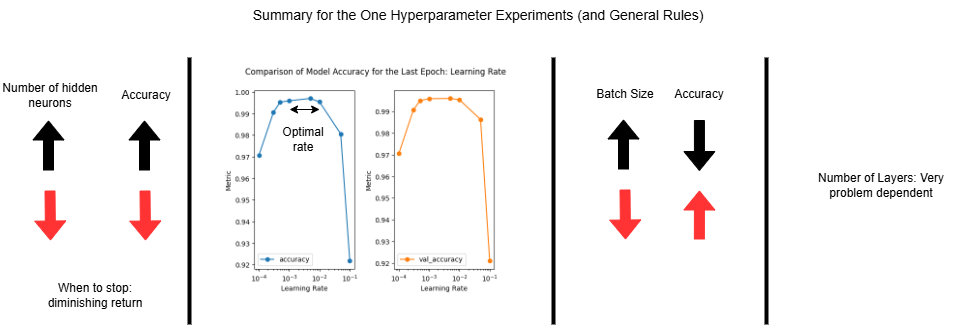
Post-analysis of the 1st and 2nd lessons lead us to the following conclusions about each of the hyperparameters.
1) Hidden Neurons Experiment: Increasing the number of hidden neurons increases the complexity of the model. This increases the accuracy of the model, until the improvement is deemed not significant (especially compared to the additional time required). Or, until you reach the point of diminishing returns beyond which accuracy may decrease due to overfitting or practical limitations.
2) Learning Rate Experiment: Smaller learning rates converge slower, since the change in the parameters are smaller, requiring more iterations. Larger learning rates train faster, but might overshoot the optimal answer. Typically a small value is ideal, for this experiment, 0.01 or even 0.001 are good.
3) Batch Size Experiment: Increasing the batch size decreases the accuracy, but shortens the training time.
4) Layer Experiment: This hyperparameter is very problem dependent. Increasing the number of layers typically improves the model’s ability to learn more complex patterns and representations. However, it does not guarantee higher accuracy, as demonstrated in this experiment by the model with four layers underperforming one with three.
Key Points
Post-analysis focuses on analyzing the results (of a model) to better understand the behavior and improve its performance.